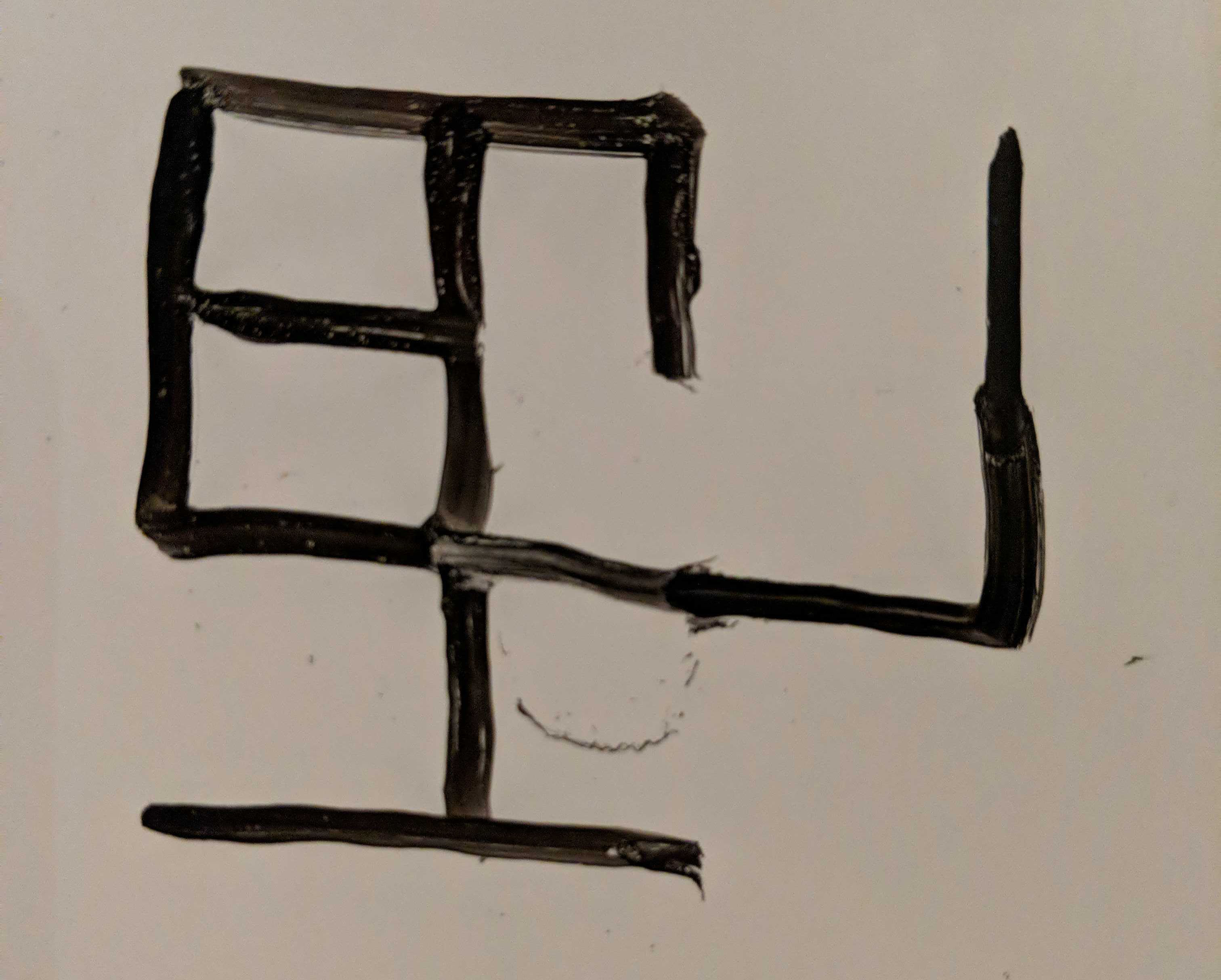Sixteen corners
06 August 2020
Last year I built a library called Picnic for rendering data tables in monospaced environments like your terminal. Part of rendering the table is calculating what character to use for each wall and each corner separating the cells.
Here’s a representative output with a bunch of different corner styles:
│ compressed │ uncompressed
├───────────┬───────────┬───────┼───────────┬───────────┬────────
APK │ old │ new │ diff │ old │ new │ diff
──────────┼───────────┼───────────┼───────┼───────────┼───────────┼────────
dex │ 664.8 KiB │ 664.8 KiB │ -25 B │ 1.5 MiB │ 1.5 MiB │ -112 B
arsc │ 201.7 KiB │ 201.7 KiB │ 0 B │ 201.6 KiB │ 201.6 KiB │ 0 B
manifest │ 1.4 KiB │ 1.4 KiB │ 0 B │ 4.2 KiB │ 4.2 KiB │ 0 B
res │ 418.2 KiB │ 418.2 KiB │ -14 B │ 488.3 KiB │ 488.3 KiB │ 0 B
asset │ 0 B │ 0 B │ 0 B │ 0 B │ 0 B │ 0 B
other │ 37.1 KiB │ 37.1 KiB │ 0 B │ 36.3 KiB │ 36.3 KiB │ 0 B
──────────┼───────────┼───────────┼───────┼───────────┼───────────┼────────
total │ 1.3 MiB │ 1.3 MiB │ -39 B │ 2.2 MiB │ 2.2 MiB │ -112 B
Wall border calculation is straightforward. For a vertical wall, a vertical pipe is used if either or both of the two cells wants a border, otherwise an empty space is used.1
Corner calculation is a bit more involved. A corner has four potential segments for the four cardinal directions that may be drawn. The four adjacent cells each participate in the visibility of two segments.
Corner Characters
Once the code determines the four boolean values for the four segments of a corner we need to map that to the display character. Four booleans produce sixteen possible values.
Initially I started with the naive nesting of conditionals to get it working.
return if (left) {
if (right) {
if (up) {
if (down) {
'┼'
} else {
'┴'
}
} else {
if (down) {
'┬'
} else { /*..*/ }
}
} else { /*..*/ }
}
Nesting conditionals is an optimization so that each boolean is only checked once. If we wanted, we could flatten the conditionals by repeatedly checking each boolean.
if (left && right && up && down) return '┼'
if (left && right && up && !down) return '┴'
if (left && right && !up && down) return '┬'
if (left && right && !up && !down) return '─'
// ...
The boolean type is a facade over the binary values 0 and 1. Replacing these conditionals with the corresponding binary yields familiar values: 1111, 1110, 1101, 1100, etc. These are the decimal values 15, 14, 13, 12, and so on down to 0.
Mapping the four booleans to these bits gives a decimal we can use to index into a single string which contains all the corner characters.
val corners = " ╷╵│╶┌└├╴┐┘┤─┬┴┼"
val index =
(if (down) 0b0001 else 0) or
(if (up) 0b0010 else 0) or
(if (right) 0b0100 else 0) or
(if (left) 0b1000 else 0)
return corners[index]
Much nicer!
Testing Corners
The logic of determining the four booleans and then choosing the corner character needs tests. Once again I started with the naive approach of a bunch of 2x2 tables with varying borders so that the middle corner was different in each.
@Test fun borderLeftRightUpDown() {
val table = table { /*..*/ }
assertThat(table.renderText()).isEqualTo("""
|1│2
|─┼─
|3│4
|""".trimMargin())
}
@Test fun borderLeftRightUp() {
val table = table { /*..*/ }
assertThat(table.renderText()).isEqualTo("""
|1│2
|─┴─
|3 4
|""".trimMargin())
}
Needing sixteen different tests feels very much like the nested conditionals above. Sure it’s correct, but can we do better? That was the question I presented to two friends who had already been watching me build the library.
(At this point I think they know to just stand back as I fall down these rabbit holes.)
What do you think? Feel free to give it a try! Scroll down for the answer…
1111…
1110…
1101…
1100…
1011…
1010…
1001…
1000…
0111…
0110…
0101…
0100…
0011…
0010…
0001…
0000!
After about 10 minutes at the whiteboard I managed to come up with a configuration that worked.
This translates nicely into a single test.
@Test fun allCorners() {
val table = table { /*..*/ }
assertThat(table.renderText()).isEqualTo("""
|┌─┬─┐ ╷
|│1│2│3│
|├─┤ ╵ │
|│4│5 6│
|└─┼───┘
| 7│8 9
|╶─┴─╴
|""".trimMargin())
}
The number of theoretical arrangements of corners is 16!, or 20,922,789,888,000, so finding a solution felt like a nice win.
This post was supposed to stop here, but…
Finding All Possible Arrangements
I did the above work a year ago, but upon seeing the very large value of 16! in preparing the post I began to wonder how many valid arrangements exist.
Once again starting naive, I wrote a recursive function which created permutations of the numbers [0,15] and then did a validation pass to see if all corresponding corners had matching edges.
(0 until 16)
.permutationSequence() // <-- produces Sequence<IntArray>
.filter { validateCorners(it) }
.forEach { println(it.contentToString()) }
This was exorbitantly slow. I let it run for an hour, and it never got far enough to find a single match.
Instead of validating each complete permutation, huge sets of permutation candidates could immediately be rejected as soon as two corners were invalid. For example, if the very first corner (upper left) has a left or up segment we can immediately reject it and eliminate 15! candidates.
fun validTables(): Sequence<IntArray> = sequence {
val state = IntArray(16)
suspend fun SequenceScope<IntArray>.placeCorner(index: Int) {
if (index == 16) {
yield(state.clone())
return
}
for (corner in 0 until 16) {
// TODO validate corner fits here!
state[index] = corner
placeCorner(index + 1)
}
}
placeCorner(0)
}
Instead of using a two-dimensional array to map the 4x4 grid it is flattened into a single 16-element array.
Since each corner needs to be different, we need to track which of the 16 were already used. This could be done with a Set<Int> but that would require allocation. Since the range of values is [0,15] and we only need to store a boolean value we can once again turn to using bits in a single Int.
fun validTables(): Sequence<IntArray> = sequence {
val state = IntArray(16)
- suspend fun SequenceScope<IntArray>.placeCorner(index: Int) {
+ suspend fun SequenceScope<IntArray>.placeCorner(index: Int, used: Int) {
if (index == 16) {
yield(state.clone())
return
}
for (corner in 0 until 16) {
+ if (used.hasBit(corner)) continue
+
// TODO validate corner fits here!
state[index] = corner
- placeCorner(index + 1)
+ placeCorner(index + 1, used.withBit(corner))
}
}
- placeCorner(0)
+ placeCorner(0, 0)
}
+
+fun Int.hasBit(bit: Int) = ((1 shl bit) and this) != 0
+fun Int.withBit(bit: Int) = (1 shl bit) or this
There are three constraints for placing a corner at the current index that must be validated:
-
If the corner is at the edge of the square, no corner segment must be present in the direction of the edge.
For example, index 0 which is at the top and left edge of the 4x4 cannot be
├because it has an up segment. -
If there is a corner to the left of the current index in the 4x4 grid, this corner can only have a left segment if that corner has a right segment.
For example, if
┐is at index 1 then┬is invalid for index 2 since they do not agree about the presence of a horizontal segment. -
If there is a corner above the current index in the 4x4 grid, this corner can only have an up segment if that corner has a down segment.
For example, if
╶is at index 0 then├is invalid for index 4 since they do not agree about the presence of a vertical segment.
In the same way four booleans were used as bits to create the numbers [0,15] in the first section, we can invert that operation to extract the four booleans from the numbers to perform validation.
fun Int.hasDownSegment() = (0b0001 and this) != 0
fun Int.hasUpSegment() = (0b0010 and this) != 0
fun Int.hasRightSegment() = (0b0100 and this) != 0
fun Int.hasLeftSegment() = (0b1000 and this) != 0
With these helpers we can add the validation.
for (corner in 0 until 16) {
if (used.hasBit(corner)) continue
- // TODO validate corner fits here!
+ if (index > 11 && corner.hasDownSegment()) continue // Bottom row
+ if (index % 4 == 3 && corner.hasRightSegment()) continue // Right column
+
+ // Find the previous row and column corners so we can test if the current corner can fit at
+ // this position. Use 0 when in top row or left column since it will always be incompatible.
+ val previousRowCorner = if (index % 4 == 0) 0 else state[index - 1]
+ val previousColCorner = if (index < 4) 0 else state[index - 4]
+
+ if (previousRowCorner.hasRightSegment() != corner.hasLeftSegment()) continue // Horizontal mismatch
+ if (previousColCorner.hasDownSegment() != corner.hasUpSegment()) continue // Vertical mismatch
state[index] = i
placeCorner(index + 1, used.withBit(i))
}
With no allocation and being able to quickly reject massive sets of invalid candidates this should hopefully produce results in less than an hour. Let’s run it!
fun main() {
val time = measureTimeMillis {
validTables().forEachIndexed { index, corners ->
val table = corners.map { " ╷╵│╶┌└├╴┐┘┤─┬┴┼".get(it) }
.joinToString("")
.chunked(4)
.joinToString("\n")
println("#${index + 1}: ${state.contentToString()}\n$table\n")
}
}
println("Done. Took $time milliseconds.")
}
Survey says?
#1: [0, 1, 4, 8, 5, 15, 12, 9, 3, 7, 13, 11, 2, 6, 14, 10]
╷╶╴
┌┼─┐
│├┬┤
╵└┴┘
...
#652: [5, 13, 12, 9, 7, 15, 8, 3, 6, 11, 1, 2, 4, 14, 10, 0]
┌┬─┐
├┼╴│
└┤╷╵
╶┴┘
Done. Took 57 milliseconds.
Considerably faster than taking hours! Only 652 valid candidates out of 20,922,789,888,000 possible permutations. You can check out the full list here.
If we look at output #1 above, this table is technically invalid since it contains an orphan corner in the upper right. There is no way to create such a corner by setting borders on table cells. However, purely from a segment-validation standpoint it is valid. Visual inspection of the candidates makes it seem like about 15-25% suffer from this case.
I’m out of time on this post, so finding the true number of valid configurations expressible by table cell borders will have to be an exercise left to the reader.
Creating Picnic was a fun rabbit hole to fall into for a few days last year. Aside from the challenges of corners, it implements the CSS specification for measuring and laying out tables and supports row and column spans, vertical and horizontal text alignment, and vertical and horizontal cell padding.
If you ever need to display a command-line table and have written an HTML table in your life it should be very approachable with Picnic.
-
It’s actually little more complicated than this. If none of the rows want to draw a border between the two cells in these columns then the border width will be zero and won’t occupy any space. ↩
— Jake Wharton